Une onde est une variation (ou perturbation) qui transfère de l’énergie progressivement d’un point à un autre dans un milieu et qui peut prendre la forme d’une déformation élastique, d’une variation de pression, d'intensité électrique ou magnétique, de potentiel électrique ou de température.
Concernant l’acoustique (aérienne), l’onde est une variation de pression.
L’onde acoustique modifie très légèrement la pression statique. L’oreille humaine ne perçoit que ces variations (0,2 % de la pression statique notée $P_{stat}$).
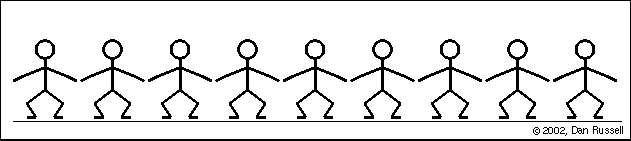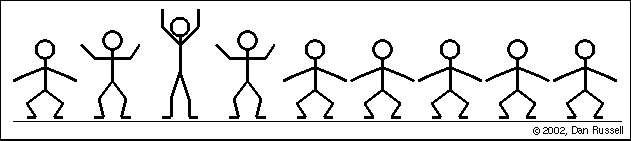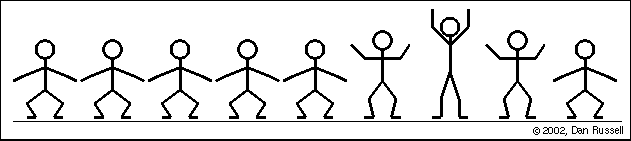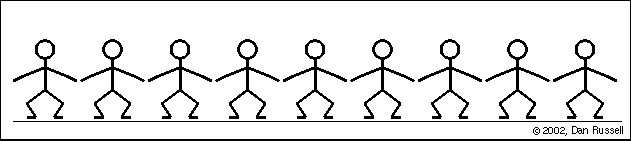
Une onde est une perturbation qui se déplace d'un endroit à un autre et est décrite par une fonction d'onde qui est fonction à la fois de l'espace et du temps. Si la fonction d'onde était une fonction sinusoïdale, l'onde serait excitée par :
$s(x,t) = A\sin(\omega t \pm kx)$
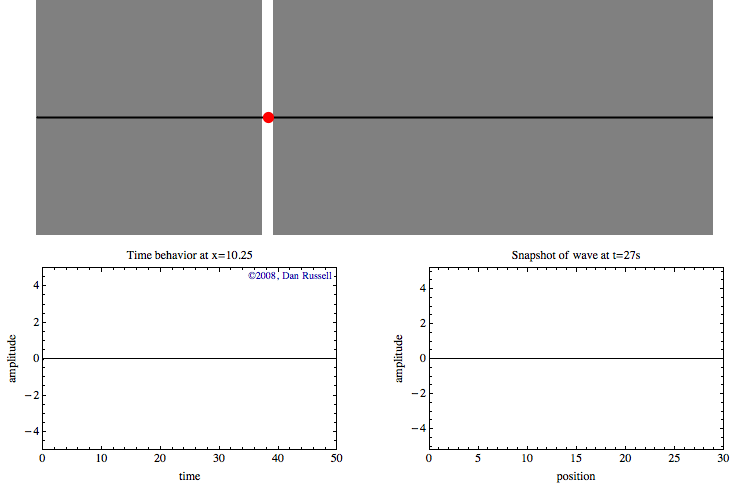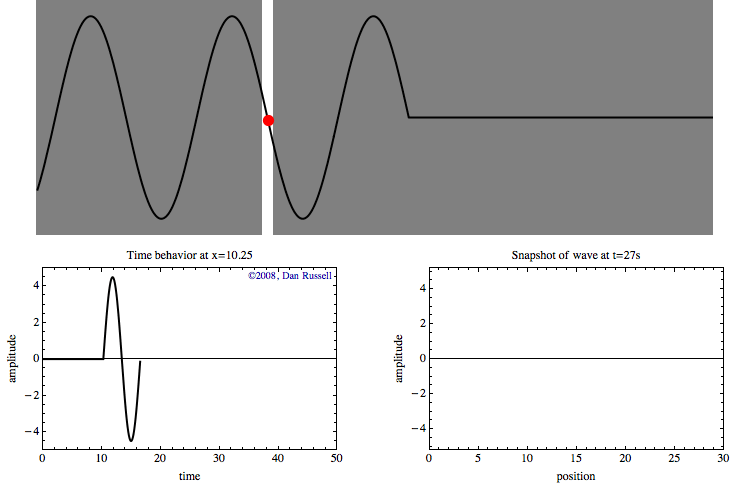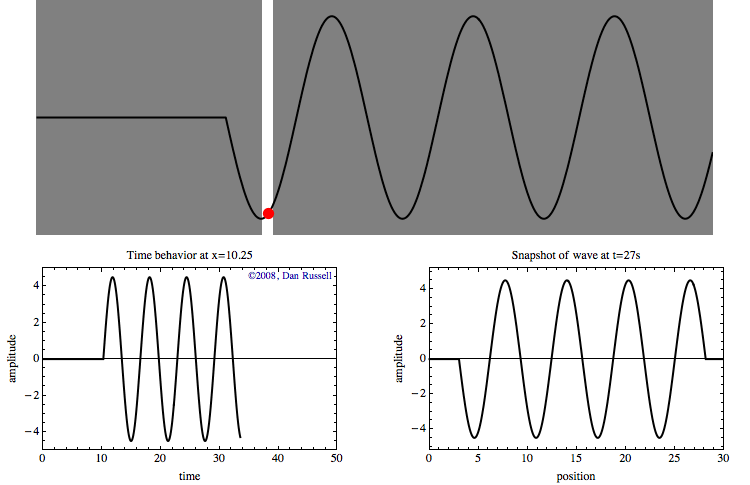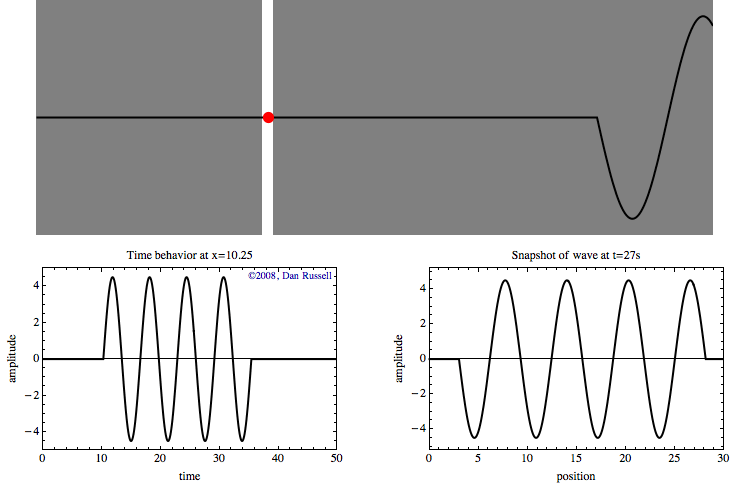
Le graphique en bas à gauche montre l'historique temporel du mouvement de ce point rouge au fil de l'onde. Ce graphique représente l'onde en fonction du temps pour un emplacement spécifique. Rien ne se passe pendant les premières secondes jusqu'à ce que le bord d'attaque de l'onde atteigne l'emplacement du point rouge. Une fois que l'onde atteint cet endroit, le point rouge oscille de haut en bas avec le temps lorsque la vague passe. Une fois l'impulsion d'onde passée, le déplacement revient à zéro.
Le graphique en bas à droite représente l'onde en fonction de la position à un moment précis (ici à 27 secondes).
La fréquence de l'onde est la rapidité avec laquelle la particule oscille autour de sa position moyenne. Elle correspond au nombre de périodes par unité de temps, c'est-à-dire l'inverse de la période. Son unité est l'Hertz (Hz ⇔ $s^{-1}$).
$f = \frac{1}{T}$
La longueur d’onde est la distance séparant deux molécules successives dans le même état vibratoire (même pression et vitesse acoustique) ou encore la distance parcourue par l’onde pendant une période.
$\lambda = \frac{c}{f}$
| | L'oreille humaine ne perçoit que les faible variations de la pression statique (0,2 % de la pression statique notée $P_{stat}$)
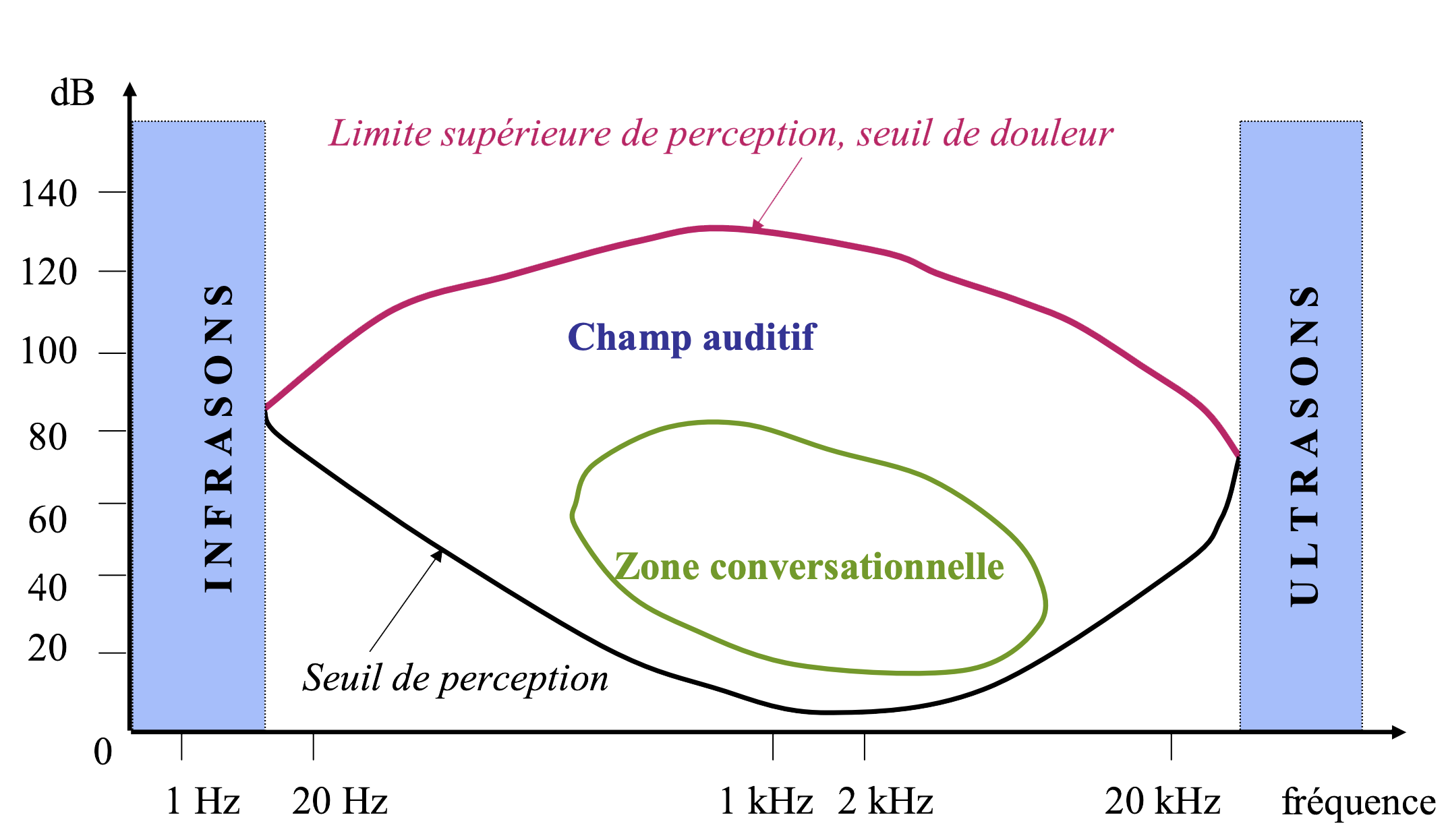
L'oreille humaine entend (dans l'air) des fréquences comprises entre 20 Hz (fréquence la plus grave) et 20 000 Hz (fréquence la plus aiguë). La dynamique de l'oreille est de : - • seuil d’audition : $2.10^{-5}$ Pa (cette valeur est aussi nomée $p_0$)
- • seuil de douleur : $200$ Pa
|
|
⚠️ L’oreille est sensible à l’amplitude de la pression acoustique efficace : $p_{eff} = \sqrt{\frac{1}{T}\int^T_0p^2_{ac}(t)dt}$.
Les appareils de mesure ne fournissent que des valeurs efficaces.
|
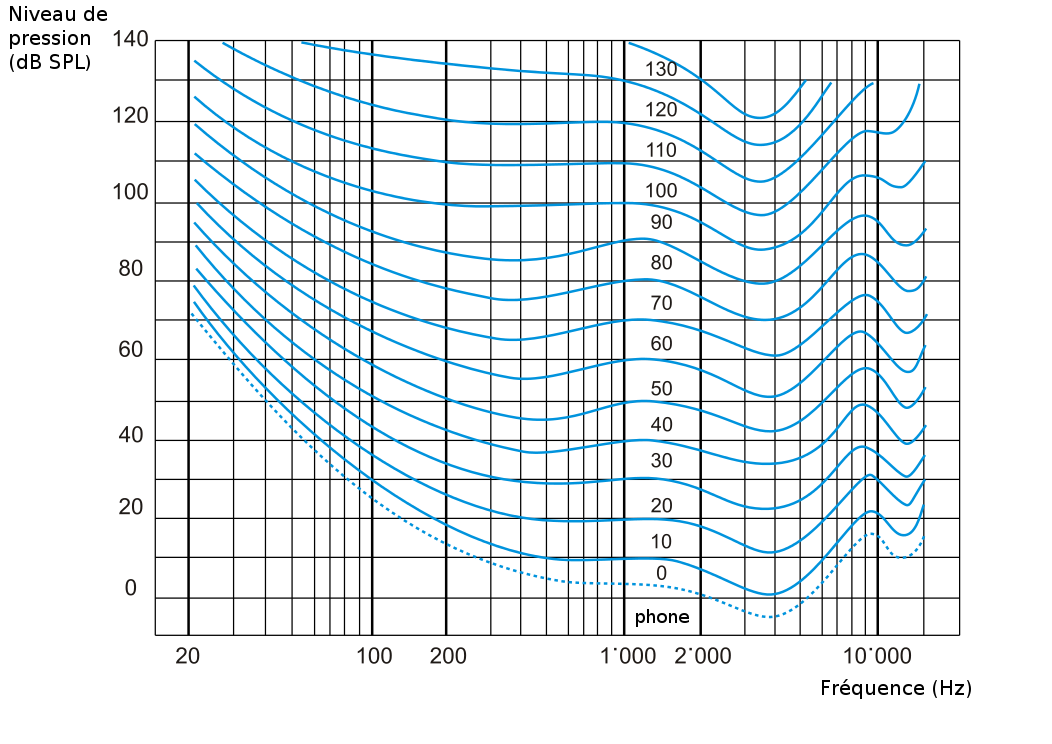
| La réponse en fréquence de l'oreille humaine n’est pas plate et elle dépend du niveau acoustique. Cela est dû notamment aux résonances de l’oreille externe dans le médium, qui amplifie la pression sonore appliquée au tympan dans cette partie du spectre. Fletcher et Munson ont tracé les courbe isosonique représentant ce phénomène.
Avec la pression sonore en ordonnée et les fréquences en abscisse, les courbes d’isosonie permettent de comparer, à sensation de volume identique, la pression sonore nécessaire selon la fréquence.
La sensibilité de l’oreille est la plus grande aux fréquences moyennes autour de 2 000 Hz, qui correspondent aux fréquences conversationnelles.
Les recherches de Fletcher et Munson, publiées en 1933, ont été poursuivies avec un protocole différent par Robinson et Dadson (1956) puis l’institut international de standardisation (ISO) a compilé les résultats d’études plus récentes menées dans un grand nombre de pays en respectant un protocole homogène et amélioré. Il a ainsi pu donner une actualisation des courbes d’égale sensibilité en 2003 (ISO 226-2003). |
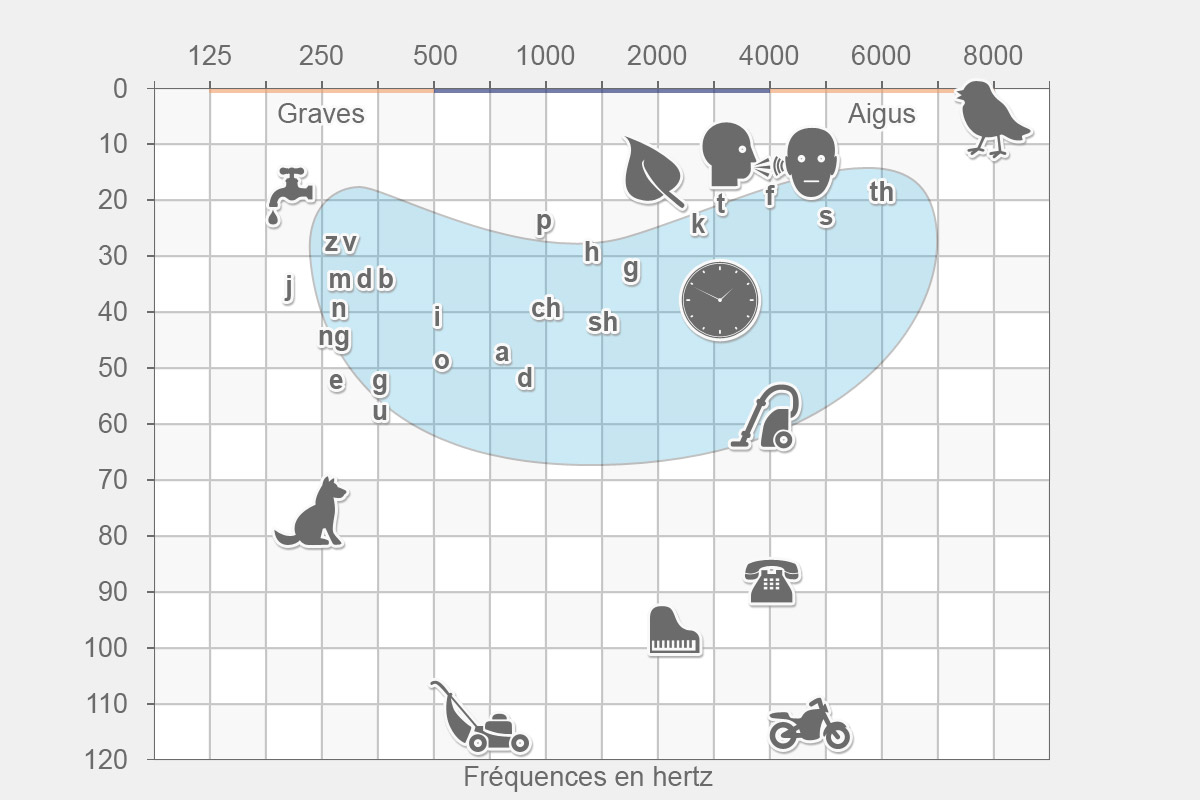
| | Lors d'une discussion, la bande des fréquences émises est couramment appelée zone des fréquences conversationnelles. Oscillant entre 500 et 4 000 Hertz, il s'agit de la zone fréquentielle la plus sensible du champ auditif. |
|
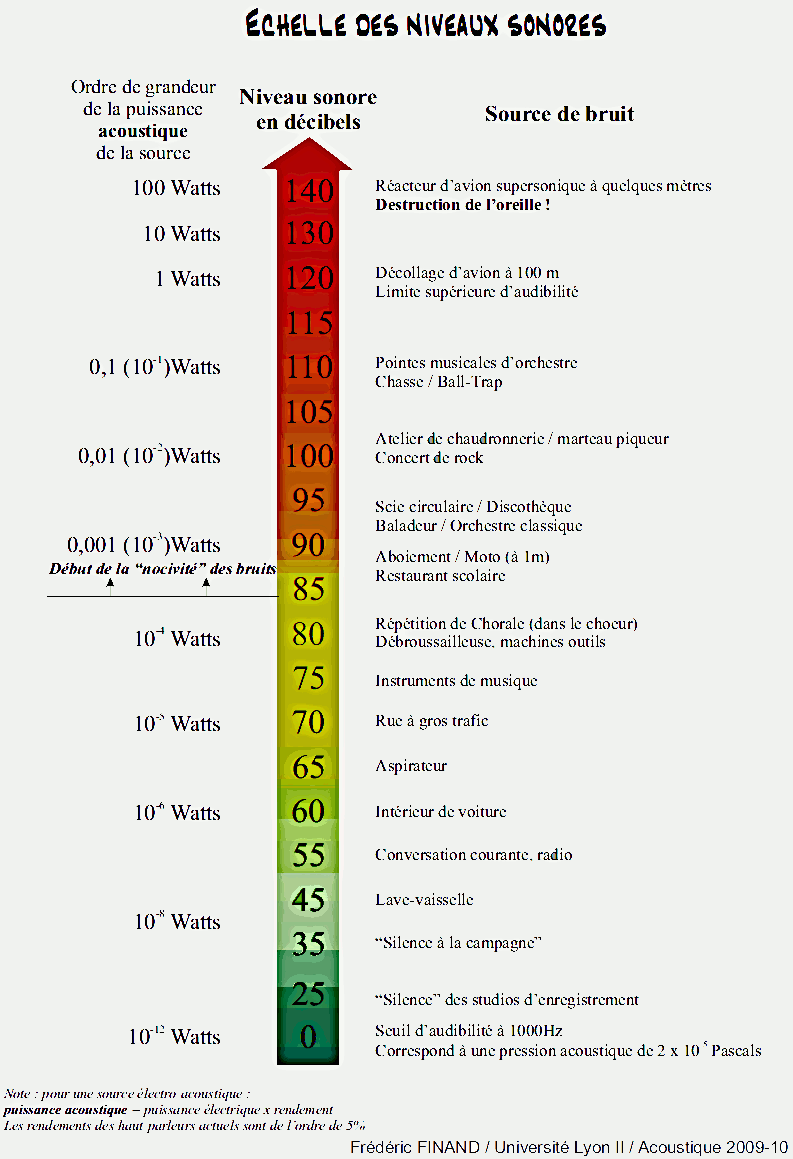
Le niveau sonore est défini par le rapport, exprimé en décibel, de l’intensité acoustique perçue par une intensité acoustique de référence correspondant au seuil d’audition à 1 kHz :
$L = 10\log\left(\frac{I}{I_0}\right) \Longleftrightarrow 20\log\left(\frac{p}{p_0}\right)$ dB SPL
avec $I_0 = 10^{-12}$ W/m$^2$ et $p_0 = 2.10^{-5}$ Pa
SPL pour Sound Pressure Level
⚠️ Les différent types de décibel (dB) sont des unités de grandeur sans dimension.
Ainsi L = 0 dB SPL ne correspond pas à "pas de son ", mais au bruit minimum (= seuil d'audibilité) que l'oreille humaine peut entendre.
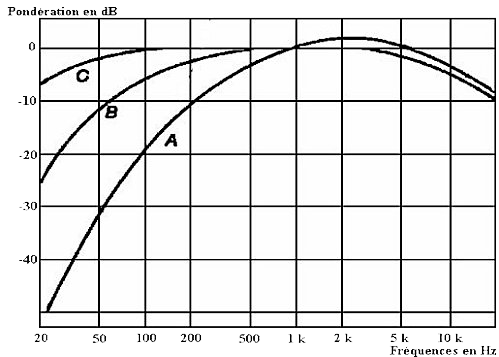
La réponse en fréquence de l'oreille humaine n’étant pas plate et dépendant du niveau acoustique, il existe un système de filtres de pondération qui prennent en compte la perception de l’oreille.
La pondération A : le dB(A)
Afin de tenir compte de cette sensibilité différente de l’oreille selon les fréquences, une unité physiologique de mesure du niveau sonore a été créée : le décibel A ou dB(A), qui intègre une pondération des niveaux de bruit selon les fréquences (courbe de pondération A). Cette pondération est basée sur la courbe isosonique à 40 phones.
| Bandes d’octave (en Hz) |
63 | 125 | 250 | 500 | 1 000 | 2 000 | 4 000 | 8 000 | 16 000 |
| Corrections A (en dB) |
-26,2 | -16,1 | -8,6 | -3,2 | 0 | 1,2 | 1 | -1,1 | -6,6 |
Le dB(A) est le plus couramment utilisé pour les mesures de bruit dans l'environnement et en milieu
industriel. Il offre, en général, une bonne corrélation entre le phénomène physique qu’est le bruit et la
sensation ressentie par une personne. Il est en outre représentatif de la perception humaine au niveau
conversationnel.
La pondération C : le dB(C)
La pondération C examine d'avantage l’effet des sons basse fréquence sur l’oreille humaine par rapport à la pondération A et est essentiellement plate ou linéaire entre 31,5 Hz et 8 kHz. Cette pondération est basée sur la courbe isosonique à 110 phones.
| Bandes d’octave (en Hz) |
63 | 125 | 250 | 500 | 1 000 | 2 000 | 4 000 | 8 000 | 16 000 |
| Corrections C (en dB) |
-0,8 | -0,2 | 0 | 0 | 0 | -0,2 | -0,8 | -3,0 | -8,5 |
Pour des niveaux sonores plus importants (supérieurs à 85 dB), l’utilisation du filtre de pondération C
doit être privilégiée. Ce filtre prend en compte la sensibilité de l’oreille humaine qui augmente pour les
basses fréquences au fur et à mesure que le niveau sonore global s’élève.
La pondération Z : le dB(Z)
La pondération Z est la réponse en fréquence plate de 8 Hz à 20 kHz, c’est le bruit réel qui est produit sans aucune pondération pour l’oreille humaine (Z pour zéro). Souvent utilisé dans l’analyse de bande d’octave et pour déterminer le bruit environnemental. Correspond donc au dB SPL.

|
| Les sources de bruit, en règle générale, sont incohérentes. Dans ces conditions, la quantité physique à sommer est la pression acoustique efficace au carré.
Si les sources sont cohérentes, la pression acoustique totale dépend du déphasage entre les sources.
Du fait de l’utilisation de cette échelle logarithmique, les décibels ne s’additionnent pas de façon arithmétique.
\[L_{t} = 10\log\left(\sum_{i} {1O} ^{\frac{L_i}{10}}\right) \]
| Augmenter le niveau sonore de : | C’est multiplier l'énergie sonore par : | C'est faire varier la sensation auditive : |
|---|
| 3 dB | 2 | Légèrement : on fait la différence entre deux lieux où le niveau diffère de 3 dB, mais il faut tendre l’oreille. |
| 5 dB | 3 | Nettement : on ressent une aggravation ou on constate une amélioration lorsque le bruit augmente ou diminue de 5 dB. |
| 10 dB | 10 | Comme si le bruit était deux fois plus fort. |
|---|
| 20 dB | 100 | Comme si le bruit était 4 fois plus fort. Une variation de 20 dB peut réveiller ou distraire l’attention. |
| 50 dB | 100 000 | Comme si le bruit était 30 fois plus fort. Une variation brutale de 50 dB fait sursauter. |
|
Global signifie une seule valeur, et non pas une courbe ou un tableau de valeurs. La méthode pour obtenir un niveau global à partir des valeurs par bandes consiste à effectuer la sommation logarithmique des valeurs par bande d'octave (ou tiers d'octave): \[L_{t} = 10\log\left(\sum_{i} {1O} ^{\frac{L_i}{10}}\right) \]
Pour un niveau global en dB(A), il faut d'abord ajouter algébriquement la valeur obtenue sur la courbe de pondération à celle du niveau par bande (octave ou 1/3), puis effectuer le calcul du niveau global dB(A) avec la relation.
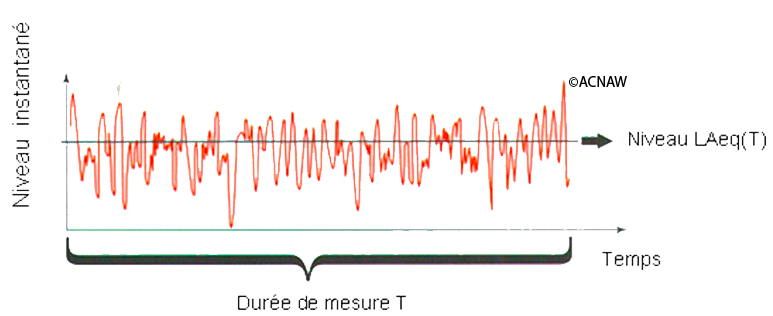
Pour caractériser une nuisance due à une exposition de durée importante à un bruit variable dans le temps, on utilise la notion de niveau sonore équivalent noté $L_{\text{eq,T}}$, ou $L_{\text{A}_{\text{eq,T}}}$ (en dBA). Il s'agit d'un indicateur statistiques de bruit pour représenter l’impact « moyen » ou « intégré » du bruit. Le niveau équivalent correspond à la moyenne « énergétique » du bruit analysé sur un intervalle de temps d’observation bien défini, de durée T.
| | Le niveau sonore $L_{\text{A}_{\text{eq,T}}}$ est défini par : \[ L_{\text{A}_{\text{eq,T}}} = 10\log\left[\frac{1}{t_2-t_1}\int^{t_2}_{t_1}\frac{p^2_{\text{A}}(t)}{p^2_0}dt\right] \]
Cette quantité se mesure directement avec un sonomètre adapté, ou après enregistrement, avec un logiciel spécialisé. On peut également faire le calcul. |
|
Ce niveau est très régulièrement utilisé comme indicateur de gêne. On observe en effet, dans la pratique, une bonne corrélation entre cette valeur et la gêne auditive ressentie par un individu exposé au bruit.
Le Leq est utilisé, de manière réglementaire, pour des types de bruits très différents :
• exposition aux bruits pendant les périodes de travail, dans l'industrie, sur les chantiers, etc : valeur maximale 85 dB(A) sur toute la journée pour le travailleur (droit du travail)
• niveaux sonores dans les "établissements diffusants de la musique" , discothèques, lieux de concerts : maximum de 105 dB(A) sur la durée de présence du public, en tout point accessible au public
• gêne due aux bruits de trafic routier et ferroviaire : lorsqu'une voie de circulation nouvelle est construite, elle ne doit pas engendrer un Leq supérieur à 60 dB(A) en façade (à l'extérieur) d'une habitation en période de jour ; la particularité des bruits de trafic automobile est que la fonction $L(t)$ est une loi statistique ("de Gauss") qui a une moyenne et une distribution constante, ce qui engendre qu'une mesure assez courte, de quelques minutes selon le trafic, suffit pour obtenir un résultat reproductible, et faire des comparaisons. Mais ce n'est pas le cas pour le trafic ferroviaire.









